I – Propagation rectiligne de la lumière :
1. Principe de propagation rectiligne de la lumière :
Dans un milieu transparent et homogène (cela veut dire que les propriétés du milieu sont les mêmes en tous les points), la lumière se propage en ligne droite.
2. Rayons et faisceaux lumineux :
Modèle du rayon lumineux :
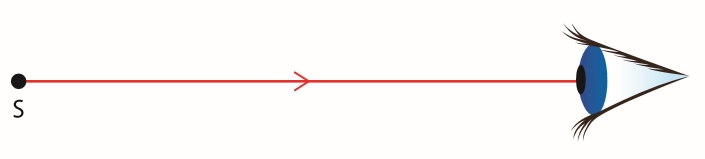
Le trajet de lumière, depuis la source lumineuse jusqu’à l’objet éclairé peut être modélisé par des demi-droites munies d’une flèche indiquant le sens de propagation.
Ces demi-droites fléchées sont appelées des rayons lumineux.
Faisceaux lumineux :
Un faisceau de lumière est constitué d’une infinité de rayons lumineux provenant d’une même source.
Les bords du faisceau lumineux sont représentés par ses rayons limites :
II – Formation des ombres :
On appelle source ponctuelle une source lumineuse dont les dimensions sont très petites par rapport aux dimensions de l’objet, pour laquelle, vue depuis l’objet, tout se passe comme s’il n’y avait qu’un point qui émet de la lumière.
Observations :
On observe qu’une partie seulement de la sphère est éclairée.
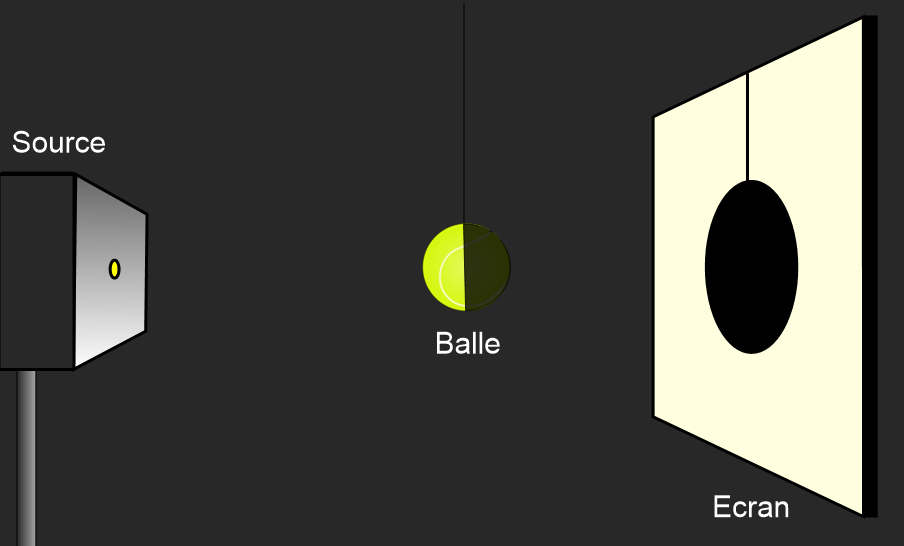
La zone sombre du corps opaque est appelée l’ombre propre.
Plaçons maintenant un écran derrière la sphère. On observe sur cet écran une partie non éclairée, de contour circulaire, appelée ombre portée de la sphère.
Entre l’écran et la balle de tennis, introduisons une balle de tennis de table. Nous pouvons localiser une zone de l’espace où cet objet n’est pas éclairé par la source : c’est la zone d’ombre ou le cône d’ombre de la sphère.
Interprétation :
La formation des ombres s’explique par le principe de propagation rectiligne de la lumière.
Représentons en utilisant le modèle du rayon lumineux une vue de profil de cette expérience, ainsi qu’une vue de face de l’écran :


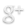




Pour un résumé d’un cours c’est très bien, il n’y a pas de mot difficile, tout est expliqué
C’est bon
Jeoeuehieie
jai aimez le traveille merci pour otre effort
J’adore votre travaille!
Mille fois merci!
Merci beaucoup pour le travail
Merci beaucoup
Merci c’est court et
bref e
salam cest tres bien jadore mais cest nul en faite
J’adore votre travaille et merci beaucoup!